Bài giảng Hình học Lớp 7 - Tiết 39: Các trường hợp bằng nhau của tam giác vuông. Luyện tập

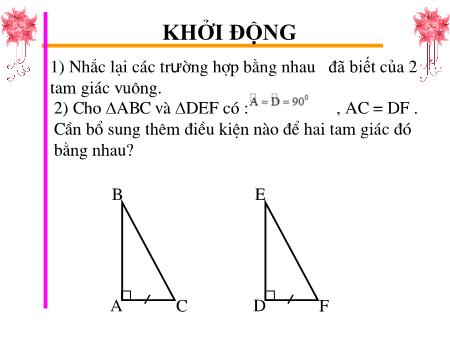
 KHỞI ĐỘNG 
1) Nh¾c l¹i c¸c trưêng hîp b»ng nhau đã biết cña 2 
tam gi¸c vu«ng. 
2) Cho ABC vµ DEF cã : Aµ == Dµ 90 0, AC = DF . 
CÇn bæ sung thªm ®iÒu kiÖn nµo ®Ó hai tam gi¸c ®ã 
b»ng nhau?
 B E
 A C D F Tiết 39. CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG. LUYỆN TẬP
1) Các trường hợp bằng nhau đã biết của hai tam giác vuông
 B E
 Nếu hai cạnh góc vuông của 
 tam giác vuông này bằng hai 
 cạnh góc vuông của tam giác 
 vuông kia thì hai tam giác vuông 
 đó bằng nhau A C c.g.c D F
 Nếu một cạnh góc vuông và một B E
 góc nhọn kề cạnh ấy của tam giác 
 vuông này bằng một cạnh góc 
 vuông và một góc nhọn kề cạnh ấy 
 của tam giác vuông kia thì hai tam 
 giác vuông đó bằng nhau A C D F
 g.c.g
 B E
 - Nếu cạnh huyền và một góc 
 nhọn của tam giác vuông này 
 bằng cạnh huyền và một góc 
 nhọn của tam giác vuông kia thì 
 hai tam giác vuông đó bằng A C D F
 nhau Cạnh huyền- góc nhọn B E • Hai tam giác 
 vuông ABC và 
 10 DEF có
 • AC = DF = 6cm;
A 6 C
 D F • BC=EF = 10cm;
 D
 • ABC = DEF 
 6
 • Em hãy dự đoán: 
 F 10 E
 hai tam giác này 
 có bằng nhau 
 không? A D
 b b
 a a
 C B F E
 Ta có ∆ABC có A = 900 nên Ta có ∆DEF có D = 900 nên
 2 2 2
BC2=+ AB 2 AC 2 (định lý Py ta go) EF=+ DE DF (định lý Py ta go)
 a2 = DE 2 + b 2
 a2 = AB 2 + b 2
 DE2 = a 2 − b 2 (2)
 AB2 = a 2 − b 2 (1)
 Từ (1) và (2) 
 Vậy ∆ABC = ∆DEF (c.c.c) hoặc ∆ABC = ∆DEF (c.g.c) Bài tập 64/ 136 
 Các tam giác vuông ABC và DEF có A = D = 900; 
 AC = DF. Hãy bổ sung thêm một điều kiện bằng 
 nhau (về cạnh hay về góc) để ABC = DEF?
 CẦN THÊM ĐIỀU KIỆN
 B E
 1) Về cạnh :
 a) AB = DE (theo trường hợp c-g-c)
 Hoặc b) BC = EF ( theo trường hợp c.h – cgv )
 2) Về góc :
A C D F
 C = F (theo trường hợp g-c-g)
 LuËt ch¬i: Cã 4 hép quµ kh¸c nhau, trong mçi hép quµ 
chøa c©u hái vµ mét phÇn quµ hÊp dÉn. NÕu tr¶ lêi ®óng 
c©u hái th× mãn quµ sÏ hiÖn ra. NÕu tr¶ lêi sai th× mãn 
quµ kh«ng hiÖn ra. Thêi gian suy nghÜ cho mçi c©u lµ 10 
gi©y. 
 hdvn PhÇn thưëng lµ:
 1 cây viết PhÇn thưëng lµ:
Mét trµng ph¸o tay PhÇn thưëng lµ:
 Cây kẹo Tiết 38. CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG
 HOẠT ĐỘNG NHÓM
 Nhóm 1,3,5. Cho ∆ABC vuông ở A. Nhóm 2,4,6. Cho ∆DEF vuông ở D. 
 Tính AB biết BC =a, AC =b Tính DE biết EF =a, DF =b
 A D
 b b
 a a
 C B F E
LG: Ta có ∆ABC có A = 900 nên LG: Ta có ∆DEF có D = 900 nên
 2 2 2
 BC2=+ AB 2 AC 2 (định lý Py ta go) EF=+ DE DF (định lý Py ta go)
 a2 = DE 2 + b 2
 a2 = AB 2 + b 2
 2 22
 22 DE = −
 AB2 =ab − ab
 Hai ∆ABC và ∆DEF có bằng nhau không? Vì sao?
 ∆ABC = ∆DEF (c.c.c) hoặc ∆ABC = ∆DEF (c.g.c) HƯỚNG DẪN TỰ HỌC.
- Học và nắm chắc các trường hợp bằng nhau của hai tam giác vuông. 
*Lưu ý hai trường hợp đặc biệt:
+ cạnh huyền –góc nhọn 
+ cạnh huyền-cạnh góc vuông.
 - Làm bài tập 63,65, 66- Sgk/Trang 136,137
 -Chuẩn bị bài tiết sau: Luyện tập. Bài 63 Cho ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh 
 rằng:
 a, HB=HC; b, BAH= CAH
 A
 a, ABH = ACH (cmt)
 Suy ra: HB=HC( hai cạnh tương ứng) 
 b, ABH = ACH (cmt)
 Suy ra: ( hai góc tương ứng) 
 BAH= CAH B H C