Bài tập ôn tập Toán Lớp 9 - Chủ đề: Đường tròn. Bài 1 đến 4 - Trường THCS Bình Tây

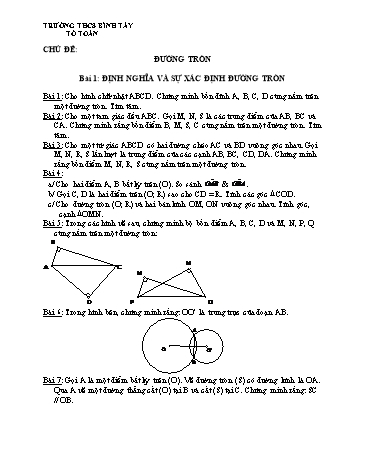
 TRƯỜNG THCS BÌNH TÂY
 TỔ TOÁN
CHỦ ĐỀ:
 ĐƯỜNG TRÒN
 Bài 1: ĐỊNH NGHĨA VÀ SỰ XÁC ĐỊNH ĐƯỜNG TRÒN
Bài 1: Cho hình chữ nhật ABCD. Chứng minh bốn đỉnh A, B, C, D cùng nằm trên 
 một đường tròn. Tìm tâm.
Bài 2: Cho một tam giác đều ABC. Gọi M, N, S là các trung điểm của AB, BC và 
 CA. Chứng minh rằng bốn điểm B, M, S, C cùng nằm trên một đường tròn. Tìm 
 tâm.
Bài 3: Cho một tứ giác ABCD có hai đường chéo AC và BD vuông góc nhau. Gọi 
 M, N, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh 
 rằng bốn điểm M, N, R, S cùng nằm trên một đường tròn.
Bài 4:
 a/ Cho hai điểm A, B bất kỳ trên (O). So sánh OAˆB & OBˆA.
 b/ Gọi C, D là hai điểm trên (O; R) sao cho CD = R. Tính các góc COD.
 c/ Cho đường tròn (O; R) và hai bán kính OM, ON vuông góc nhau. Tính góc, 
 cạnh OMN.
Bài 5: Trong các hình vẽ sau, chứng minh bộ bốn điểm A, B, C, D và M, N, P, Q 
 cùng nằm trên một đường tròn:
 B
 N
 A C
 M
 D P Q
Bài 6: Trong hình bên, chứng minh rằng: OO’ là trung trực của đoạn AB.
 A
 O O'
 B
Bài 7: Gọi A là một điểm bất kỳ trên (O). Vẽ đường tròn (S) có đường kính là OA. 
 Qua A vẽ một đường thẳng cắt (O) tại B và cắt (S) tại C. Chứng minh rằng: SC 
 // OB. TRƯỜNG THCS BÌNH TÂY
 TỔ TOÁN
 Bài 2: TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
Bài 1: Cho đường tròn có đường kính AB, tâm O; CD là một dây không cắt AB. 
 Từ A, B lần lượt vẽ AE, BF vuông góc với đường thẳng CD.
 a/ Chứng minh rằng CD, EF có cùng trung điểm. Suy ra CE = DF.
 b/ Tính chất trên còn đúng không lúc dây CD cắt đường kính AB.
Bài 2: Cho ABC nội tiếp trong đường tròn (O). vẽ OM  AB tại M và ON  AC 
 tại N. Chứng minh rằng : MN // BC.
Bài 3: Cho đường tròn (O) và 3 điểm A, B, C nằm trên đó sao cho tâm O nằm 
 trong ABC. Vẽ hai đường cao BM và CN cắt nhau tại H. Gọi I là trung điểm 
 cạnh BC. Chứng minh rằng : OI // AH.
Bài 4: Cho (O) và 3 điểm A, B, C nằm trên đó. Gọi M là trung điểm AB. Vẽ Mx 
 song song với BC, cắt AC tại N. Chứng minh rằng : ON  AC.
Bài 5: Cho đường tròn (O) và một điểm A ở ngoài đường tròn. Đường thẳng OA 
 cắt (O) tại B và C (B nằm giữa A, C). Gọi M là trung điểm AC. Vẽ dây HK 
 vuông góc AC tại M. chứng minh rằng : AHCK là hình thoi.
Bài 6: Gọi I là trung điểm dây AB không qua tâm của đường tròn (O; R).
 a/ Chứng minh: OI AB.
 b/ Qua I vẽ dây EF. Chứng minh : EF AB. Tìm độ dài lớn nhất, nhỏ nhất của 
 các dây quay quanh I.
Bài 7: Cho đường tròn (O), đường kính AB. Chứng minh rằng: nếu hai dây AC và 
 BD song song với nhau thì bằng nhau.
Bài 8: Cho điểm P ở bên trong (O). Dựng một dây AB qua P sao cho PA = PB.
Bài 9: Cho điểm P ở bên trong (O). Dựng đường tròn (P) sao cho (O) chia (P) 
 thành hai nửa đường tròn.
Bài 10: Cho điểm A cố định bên trong (O; R) và MN là một dây quay quanh A. 
 Chứng minh rằng: trung điểm I của các dây MN thuộc về một đường cố định.
Bài 11: Cho đường tròn (O), đường kính AB = 2R. Vẽ dây AC tạo với AB một góc 
 CAˆB 30 .
 a/ ABC là tam giác đặc biệt gì? Tính cạnh và góc?
 b/ Gọi I là trung điểm dây AC. Tính CI theo R.
Bài 12: Cho đường tròn (O; R) và hai bán kính OC, OD vuông góc nhau.
 a/ Hỏi OCD là tam giác đặc biệt gì? Tính cạnh và góc?
 b/ Suy ra cách vẽ một dây bằng R 2 của đường tròn (O; R).
Bài 13: Cho đường tròn (O) ngoại tiếp ABC có Aˆ 70 ; Cˆ 63 . Hãy sắp thứ tự 
 độ dài các cạnh AB, BC, CA và suy ra thứ tự các khoảng cách từ tâm O đến các 
 cạnh AB, BC, CA.
Bài 14: Cho đường tròn (O) và hai dây AB và CD (AB > CD) kéo dài cắt nhau tại 
 điểm P bên ngoài (O). Gọi trung điểm của AB và CD là H và K. So sánh PH và 
 PK. TRƯỜNG THCS BÌNH TÂY
 TỔ TOÁN
 a/ Chứng minh ba điểm B, C, D thẳng hàng.
 b/ Tính BC, BD biết CD = a.
Bài 7: Cho ABC nội tiếp đường tròn (O). Tia phân giác của BAˆC cắt đường tròn 
 (O) tại M. Chứng tỏ MBC cân và OM vuông góc với BC.
Bài 8: Cho ABC nội tiếp đường tròn (O). Vẽ đường cao AH và đường kính AD. 
 Chứng tỏ AB.AC = AH.AD.
Bài 9: Cho ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE 
 cắt đường tròn (O) lần lượt tại M. N. Chứng tỏ AMN cân và OA vuông góc 
 với MN.
Bài 10: Cho ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao AD, BE 
 cắt nhau tại H và cắt đường tròn (O) tại I, K.
 a/ Chứng minh: CAˆI CBˆK CBˆI b/ Chứng minh : CIK cân.
Bài 11: Cho một điểm S cố định không thuộc đường tròn (O). Qua S vẽ hai cát 
 tuyến bất kỳ SAB, SCD của đường tròn (O). Chứng tỏ SA.SB = SC.SD. Nêu 
 nhận xét tổng quát.
Bài 12: Cho ABC cân tại A, nội tiếp đường tròn (O). Qua A vẽ một cát tuyến cắt 
 dây BC tại D và cắt đường tròn (O) tại E. Chứng tỏ AB2 = AD.AE
Bài 13: Cho ABC nội tiếp đường tròn (O), đường kính AB. Từ trung điểm M của 
 cung AB vẽ dây MN song song với BC. Gọi giao điểm của MN và AC là S. 
 Chứng tỏ SA = SN, SC = SM
Bài 14: Cho một điểm M thuộc đường tròn (O), đường kính AB. Gọi Ax là tiếp 
 tuyến tại A của đường tròn (O) và C là hình chiếu của M trên Ax. Chứng minh 
 MA2 = AB.MC.
Bài 15: Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Lấy 
 một điểm M trên cung AC. Tiếp tuyến tại M gặp đường thẳng CD tại N. Chứng 
 minh rằng MNˆD 2.MBˆA
Bài 16: Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm thuộc 
 cung BC. Trên tia MA đặt MD = MB.
 a/ Hỏi MBD là tam giác gì?
 b/ So sánh BDA và BMC. Suy ra MA = MB + MC
Bài 17: Cho tam giác đều ABC nội tiếp đường tròn (O; R). Vẽ đường kính BD. 
 Tính cạnh, góc BCD. Suy ra độ dài cạnh tam giác đều nội tiếp đường tròn (O; 
 R)
Bài 18: Cho góc nhọn xAy, trên tia Ax lấy điểm B. Đường tròn có đường kính AB, 
 tâm O, cắt cạnh Ay tại C, cắt phân giác Az của xAˆy tại D.
 a/ Chứng tỏ OD và AC cùng vuông góc với BC.
 b/ AD và BC cắt nhau tại I, chứng minh IA.ID = IB.IC
 c/ Hai đường thẳng BD, AC cắt nhau tại K. Chứng minh ABK cân, có trực tâm 
 là I và KA.KC = KB.KD TRƯỜNG THCS BÌNH TÂY
 TỔ TOÁN
 Bài 4: GÓC TẠO BỞI MỘT TIẾP TUYẾN VÀ MỘT DÂY CUNG
Bài 1: Cho xAy là tiếp tuyến tại A của đường tròn (O; R) và cung AB là cung có số 
 đo bằng 900.
 a/ Tính các góc tạo bởi Ax, Ay và dây cung AB.
 b/ Chứng tỏ OB // xy và tính AB theo R.
 c/ Lấy M bất kỳ trên đường tròn (O) (M A, B), tính số đo góc AMB.
Bài 2: Cho xAy là tiếp tuyến tại A của đường tròn (O; R) và AB là dây cung tạo 
 góc xAˆB 30 .
 a/ Tính AOˆB , suy ra độ dài dây AB theo R.
 b/ Lấy điểm M bất kỳ trên đường tròn (O) khác A, B, tính góc AMB.
 c/ Đường thẳng OB cắt xy tại C và cắt đường tròn (O) tại D (D B). Tính CA, 
 CO theo R, chứng tỏ ACD cân và tính diện tích ACD theo R.
Bài 3: Cho ABC đều nội tiếp đường tròn (O; R) và xBy là tiếp tuyến tại B của 
 đường tròn này.
 a/ Tính các góc tạo bởi Bx, By và dây cung BC.
 b/ Chứng minh xy // AC.
Bài 4: Cho đường tròn (O; R), đường kính BC. Vẽ dây AB = R 3 .
 a/ Chứng tỏ ABC là nữa tam giác đều. Tính cạnh và góc còn lại.
 b/ Tiếp tuyến tại A của đường tròn (O) cắt BC tại M. chứng minh MA2 = 
 MB.MC =3R2.
Bài 5: Cho ABC nội tiếp đường tròn (O). Một đường thẳng song song với tiếp 
 tuyến tại A của đường tròn (O), cắt hai đoạn AB, AC tại E, D. Chứng minh 
 AB.AE = AC.AD.
Bài 6: Cho ABC, giả sử trên tia đối của tia BC có điểm I sao cho IAˆB ACˆB , 
 chứng minh IA là tiếp tuyến của đường tròn (ABC) và IA2 = IB.IC.
Bài 7: Cho ABC, biết rằng trên đường thẳng BC và ở ngoại đoạn BC có điểm I 
 sao cho IA2 = IB.IC, chứng tỏ IA là tiếp tuyến của dường tròn (ABC).
Bài 8: Qua điểm S ở ngoài đường tròn (O; R) vẽ tiếp tuyến SA (A là tiếp điểm) và 
 cát tuyến SBC (B, C là giao điểm) của đường tròn (O).
 a/ Chứng minh SA2 = SB.SC = OS2 – R2. Nêu nhận xét tổng quát.
 b/ Cho biết SA = 20cm và cát tuyến dài nhất cùng qua S bằng 50cm. Tính bán 
 kính đường tròn
 c/ Cho biết OS = 2R, BC = R, tính SB, SC theo R.